양-밀스 이론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
양-밀스 이론은 1954년 양전닝과 로버트 밀스가 도입한 비가환 게이지 이론으로, 양자전기역학을 일반화하여 강한 상호작용의 아이소스핀을 설명하려 했다. 초기에는 실험 결과와 맞지 않아 잊혀졌으나, 자발 대칭 깨짐의 발견으로 표준 모형의 일부가 되었다. 양-밀스 이론은 라그랑지언으로 정의되며, 게이지 변환과 양-밀스 항을 포함한다. 이 이론은 힉스 상, 윌슨 상, 쿨롱 상 등 다양한 상을 가지며, 재규격화군을 통해 결합 상수의 변화를 설명한다. 양자화는 경로 적분을 통해 이루어지며, 페인만 도표를 사용하여 섭동 이론을 전개한다. 양-밀스 이론은 재규격화 가능하며, 현재 수학적 문제와 함께 밀레니엄 문제 중 하나인 질량 간극 가설의 증명 등 미해결 과제를 안고 있다.
더 읽어볼만한 페이지
- 게이지 이론 - 양자 색역학
양자 색역학은 색 전하를 국소 대칭으로 정의한 SU(3) 게이지 군의 비아벨 게이지 이론으로, 쿼크와 글루온을 기본 입자로 하여 쿼크 사이의 강한 상호작용을 매개하며, 점근적 자유성과 색 가둠의 특징을 가지는 이론이다. - 게이지 이론 - 점근 자유성
점근 자유성은 양자 색역학의 특징으로, 높은 에너지에서 쿼크가 자유 입자처럼 행동하며, 이는 쿼크와 글루온의 상호작용을 설명하는 양-밀스 이론의 중요한 성질이고, 높은 에너지에서는 결합 상수가 0으로 수렴하지만 낮은 에너지에서는 결합 상수가 무한대로 발산하는 색 가둠 현상과 관련되어 있다. - 양자장론 - 페르미-디랙 통계
페르미-디랙 통계는 파울리 배타 원리를 따르는 페르미 입자의 통계적 분포를 설명하는 양자 통계로, 금속 내 전자 현상 등을 이해하는 데 기여하며 페르미 입자가 특정 에너지 준위를 점유할 확률을 나타낸다. - 양자장론 - 양자 색역학
양자 색역학은 색 전하를 국소 대칭으로 정의한 SU(3) 게이지 군의 비아벨 게이지 이론으로, 쿼크와 글루온을 기본 입자로 하여 쿼크 사이의 강한 상호작용을 매개하며, 점근적 자유성과 색 가둠의 특징을 가지는 이론이다. - 물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다. - 물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.
2. 역사
양-밀스 이론은 1954년 중국의 양전닝과 미국의 로버트 밀스(Robert L. Mills)가 도입하였다.[17] 이는 최초의 비가환 게이지 이론이자 (전자기학 다음으로) 역사상 두 번째 게이지 이론이다. 양전닝과 밀스는 양자전기역학을 일반화하여, U(1) 군을 SU(n)으로 치환하였다.
양전닝은 아이소스핀 보존을 설명하려 했으나, 초기에는 실험과 맞지 않아 어려움을 겪었다. 그러나 1960년에 자발 대칭 깨짐이 발견되면서 문제가 해결되었고, 강한 상호작용의 색전하와 약한 상호작용 설명에 도입되어 표준 모형의 일부가 되었다.
2. 1. 초기 역사
양전닝과 로버트 밀스(Robert L. Mills)는 1954년에 강한 상호작용의 아이소스핀을 설명하기 위해 양-밀스 이론을 도입하였다.[1] 이는 최초의 비가환 게이지 이론이며, 전자기학 다음으로 역사상 두 번째 게이지 이론이다. 양전닝과 밀스는 양자전기역학을 일반화하여, U(1) 군을 SU(n)으로 치환하는 시도를 했다.1953년 여름, 양과 밀스는 아벨 군(예: 양자 전기역학)에 대한 게이지 이론의 개념을 비가환군으로 확장하여, 강한 상호작용과 관련된 충돌에서 아이소스핀 보존을 설명하기 위해 SU(2) 군을 선택했다.[4] 1954년 2월 프린스턴에서 양의 발표에 대해 파울리는 게이지 불변성 아이디어를 사용하여 개발된 장의 질량에 대해 질문하며 이의를 제기했다.[4] 파울리는 게이지 불변성을 적용하는 작업을 했지만, 이론의 질량이 없는 여기가 "비물리적 '그림자 입자'"가 된다고 보고 출판하지 않기로 결정했기에 이것이 문제가 될 수 있음을 알고 있었다.[2] 양과 밀스는 1954년 10월에 논문을 출판했는데, 논문의 거의 마지막 부분에서 다음과 같이 인정했다.
> 우리는 양자의 질량 문제에 도달하는데, 이에 대한 만족스러운 답을 가지고 있지 않습니다.[5]
초기 양-밀스 이론은 이 문제로 인해 어려움을 겪었으나, 1960년 자발 대칭 깨짐 개념이 도입되면서 강한 상호작용과 약한 상호작용을 설명하는 데 성공적으로 적용되었다.
2. 2. 비가환 게이지 이론 연구
1953년, 볼프강 파울리는 일반 상대성 이론의 칼루자-클라인 이론을 확장하여 6차원 이론을 공식화했다.[6] 하지만 파울리는 자신의 이론이 "다소 비물리적인 그림자 입자"를 초래한다는 것을 발견했기 때문에 자신의 결과를 공식적으로 발표하는 것을 자제했다. 파울리는 6차원 이론을 발표하지 않았지만, 1953년 11월 취리히에서 이에 대한 두 번의 세미나 강연을 했다.[1]1954년 1월, 케임브리지 대학교의 대학원생 로널드 쇼도 핵력에 대한 비가환 게이지 이론을 개발했다.[7] 그러나 이 이론은 게이지 불변성을 유지하기 위해 질량이 없는 입자를 필요로 했다. 당시에는 그러한 질량이 없는 입자가 알려져 있지 않았기 때문에, 쇼와 그의 지도교수 압두스 살람은 자신들의 연구를 발표하지 않기로 결정했다.[7] 양전닝과 밀스가 1954년 10월에 논문을 발표한 직후, 살람은 쇼에게 그의 기여를 알리기 위해 연구를 발표하도록 권유했다. 쇼는 이를 거절하고 대신 1956년에 출판된 그의 박사 학위 논문의 한 장을 구성하게 되었다.[8][9]
2. 3. 표준 모형으로의 발전
1960년 제프리 골드스톤, 남부 요이치로, 조반니 조나-라시니오는 질량 없는 이론에서 입자가 대칭성 깨짐을 통해 질량을 얻는 개념을 제시했다.[4] 이 개념은 전약 상호작용과 양자 색역학(QCD)의 공식화에 중요한 영향을 미쳐, 양-밀스 이론 연구를 다시 시작하게 했다.[4] 전약 상호작용은 게이지 군 SU(2) × U(1)으로 설명되며, QCD는 SU(3) 양-밀스 이론이다. 표준 모형은 강한 상호작용을 SU(3) × SU(2) × U(1) 대칭군을 통해 통일된 전약 상호작용(약한 상호작용과 전자기 상호작용을 통일)과 결합한다.3. 이론적 내용
양-밀스 이론은 비가환 대칭군을 갖는 게이지 이론의 특별한 예시이다. 이 이론은 바일 등에 의해 연구가 진행된 가환 대칭성에 기초한 게이지 이론을 비가환 대칭성까지 발전시킨 것이다.[2]
이 이론의 핵심 요소는 다음과 같다.
- 라그랑지안:
- 게이지 장의 라그랑지언은 로 주어진다.[2]
- 다른 입자들은 공변미분 ()을 통해 최소결합(minimal coupling)된다.
- 장방정식: 라그랑지안으로부터 고전적인 장방정식을 얻는다.
- 자기-상호작용: 이 필드는 자기-상호작용하는 속성을 가지며, 운동 방정식은 세미선형이다. 비선형성은 미분과 미분 없이 모두 존재한다.
- 섭동 이론: 이 이론은 작은 비선형성을 가진 섭동 이론으로만 관리할 수 있다.
- 차원과 재규격화:
- D차원에서 필드는 로, 결합은 로 스케일링된다.
- 4차원 초과에서는 재규격화될 수 없다.
- 스케일 불변성: 4차원에서 결합은 무차원이며, 필드와 결합의 제곱은 질량이 없는 4차 스칼라장 이론의 필드 및 결합과 동일한 차원을 갖는다. 따라서 고전적 수준에서 스케일 불변성을 공유한다.
이 이론은 파데예프-포포프 양자화를 사용하여 양자 이론으로 확장될 수 있다.
비가환 게이지 이론의 대표적인 예시로는 양-밀스 이론 외에도 천-사이먼스 이론 등이 있다.
양-밀스 이론은 원래 양성자와 중성자의 아이소스핀 SU(2) 대칭성에 착안하여 구축되었으나[13], 실험과 맞지 않았다. 하지만, 현재는 자발적으로 깨진 약 아이소스핀과 하이퍼전하의 SU(2)×U(1) 대칭성에 계승되었다고 할 수 있다 (와인버그-살람 이론).
현재 전형적인 양-밀스 이론은 색 SU(3) 대칭성에 기초한 양자색역학이며, 검증되지 않은 이론으로는 SU(5)나 SO(10) 대칭성에 기초한 대통일 이론 등이 있다. 초대칭을 갖도록 확장된 초대칭 양-밀스 이론은 초끈 이론과의 관계 등으로부터 활발하게 연구되고 있다.
3. 1. 정의
양-밀스 이론의 게이지 장의 라그랑지언은 다음과 같다.:
다른 입자에는 다음과 같은 공변미분을 정의하여 최소결합(minimal coupling)시킨다.
:
라그랑지안으로부터 고전적인 장방정식을 얻는다.
비가환 리 군을 게이지 대칭으로 가지는 게이지 이론으로 파라미터 로 특징지어지는 리 군은 다음과 같다.
:
여기서, T는 리 군의 생성자이다. 군의 비가환성을 반영하여 생성자의 리 대수는 다음과 같다.
:
f는 군의 구조 상수이다. 국소화된 매개변수 로 특징지어지는 게이지 변환 하에서, 리 군의 표현의 첨자 i를 갖는 장 는 다음과 같이 변환된다.
:
매개변수의 1차를 고려하면 다음과 같다.
:
여기서 생성자 는, 게이지 변환 하에서의 장 가 속하는 표현에서의 행렬 표현이다. 게이지 변환 하에서의 장의 변환성을 결정하는 생성자의 표현은 '''전하'''라고 불린다.
g는 이론의 '''결합 상수'''로, '''게이지 결합 상수'''라고 불린다. 이 이론의 큰 특징으로, 공변 미분이나 양-밀스 항에 포함된 모든 결합 상수가 동일하다는 점이 있다 ('''결합 상수의 보편성''').
양-밀스 이론에서 라그랑지안에 포함된 장의 미분 는 '''공변 미분'''
:
으로 대체된다. 여기서 는 게이지장이다. 게이지장은 게이지 변환 아래에서 매개변수의 일차로 다음과 같이 변환된다.
:
따라서 공변 미분은 다음과 같이 변환되어 장과 동일한 변환성을 갖는다.
:
이로 인해 다양한 장으로부터 게이지 대칭성을 만족하는 항을 만들 수 있다[16]。 여러 장들은 게이지장과 공변 미분을 통해서만 상호 작용한다. 상호 작용의 형태는 게이지 변환 하에서의 변환성에 의해 결정되며, 이러한 상호 작용의 형태는 최소 결합의 이론이라고 불린다. 양-밀스 이론에서는, 라그랑지안에 '''양-밀스 항'''
:
(각 첨자에 대해 합을 취함)을 갖는다. F는 '''게이지장 강도'''이며 다음과 같다.
:
자명하지 않은 교환 관계에 따라, 구조 상수와 관련된 항이 나타나는 것이 특징이다.
3. 2. 게이지 변환
국소화된 매개변수한국어 로 특징지어지는 게이지 변환 하에서, 리 군의 표현 첨자 i를 갖는 장 는 다음과 같이 변환된다.[16]:
매개변수의 1차 항을 고려하면 다음과 같다.
:
여기서 생성자 는 게이지 변환 하에서 장 가 속하는 표현에서의 행렬 표현이다. 게이지 변환에서 장의 변환성을 결정하는 생성자의 표현은 '''전하'''라고 불린다.
게이지 결합 상수라고 불리는 g는 이론의 결합 상수이다.
양-밀스 이론에서 라그랑지안에 포함된 장의 미분 는 다음의 공변 미분으로 대체된다.
:
여기서 는 게이지장이다.
게이지장은 게이지 변환 아래에서 매개변수의 1차 항으로 다음과 같이 변환된다.[16]
:
따라서 공변 미분은 다음과 같이 변환된다.
:
이는 장과 동일한 변환성을 갖는다.
3. 3. 양-밀스 항
양-밀스 이론의 라그랑지안에는 양-밀스 항이 포함된다.:
여기서 는 게이지장 강도(field-strength)이며 다음과 같이 정의된다.[2]
:
리 대수의 비가환성에 따라, 구조 상수와 관련된 항이 나타나는 것이 특징이다.
4. 상 (Phase)
물질을 포함하는 게이지 군이 인 양-밀스 이론에서 임의의 방향 는 다양한 상들을 가진다.[18][19][20] 이들은 퍼텐셜 로 나타낼 수 있다.
- '''힉스 상'''(Higgs phase영어)에서는 이다. 이는 상호작용이 힉스 메커니즘 등을 통해 자발 대칭 깨짐을 겪는 경우다. 이 경우, 낮은 에너지에서는 이 상호작용을 관찰할 수 없다. 표준 모형의 약한 상호작용이 이에 해당한다.
- '''윌슨 상'''(Wilson phase영어) 또는 '''가둠 상'''(confining phase영어)에서는 이다. 이 경우는 U(1)이 단순 리 군 에 속하고, 낮은 에너지에서 관측되는 입자들은 에 대하여 대전되지 않는 일중항(singlet)들이다. 표준 모형의 강한 상호작용이 이에 해당한다.
- '''쿨롱 상'''(Coulomb phase영어)에서는 (쿨롱 법칙)이다. 예를 들어, 게이지 군이 아벨 군으로 대칭 깨짐을 겪는 경우, 깨지지 않은 방향들은 이러한 상에 있게 된다. 또한, 비아벨 게이지 이론에서도 충분한 수의 페르미온이 있다면 점근 자유성이 사라지고, 쿨롱 상이 있게 된다. 표준 모형의 전자기 상호작용이 이에 해당한다.
- '''자유 전기 상'''(自由電氣相, free electric phase영어)에서는 이다. 이는 아벨 게이지 이론에서, 무질량 대전 입자가 존재하는 경우이다. 이 경우 재규격화군 흐름에 의하여 결합 상수가 로, 낮은 에너지 (긴 거리)에서 약해진다. 이는 쌍생성을 통한 진공 편극(vacuum polarization)에 의한 가리움 효과(shielding effect)이다.
- '''자유 자기 상'''(自由磁氣相, free magnetic phase영어)에서는 이다. 이는 아벨 게이지 이론에서 무질량 자기 홀극이 존재하는 경우이다. 이 경우 자기 결합 상수가 이 되므로, 두 전기 홀극 사이의 퍼텐셜은 그 역으로, 먼 거리에서 쿨롱 상보다 더 강하게 된다. 이는 자기 홀극의 쌍생성에 의한 것이다.
이들 상들은 윌슨 고리를 질서 변수(order parameter)로 갖는다. 마찬가지로, 이에 대응하는 엇호프트 고리(’t Hooft loop영어)는 혼돈 변수(disorder parameter)이다. 자이베르그 이중성에 따라, 힉스 상은 윌슨 상으로, 자유 전기 상은 자유 자기 상으로 대응된다. 쿨롱 상은 자이베르그 이중성에 대해 불변이다.
전기-자기 이중성은 힉스 상과 윌슨 상을 관계짓는다. 즉, 전기 홀극이 진공 기댓값을 가지면 힉스 상이 되고, 반대로 자기 홀극이 진공 기댓값을 가지면 윌슨 상이 된다.
5. 재규격화군과 결합 상수
재규격화군 개념을 통해, 에너지 스케일에 따라 결합 상수가 변화하는 것을 알 수 있다. 개의 맛깔을 가진 게이지 군의 표현 에 속하는 페르미온을 포함하는 양-밀스 이론의 1루프 베타 함수는 다음과 같다.[2]
:
여기서 는 에 의해 정의되는 수반 표현에서의 2차 카시미어 연산자이고, 은 표현 에서의 생성자 행렬 표현의 정규화 상수 이다.
양자 색역학에서는 이고, 이다.[2] 페르미온의 맛깔이 적은 경우, 양-밀스 이론은 고에너지에서 상호작용이 약해지는 점근적 자유성을 가진다.[2]
6. 양자화
루드비히 파데예프와 빅토르 포포프는 '고스트 장'을 도입하여 게이지 자유도 문제를 해결하였다. 이 장은 페르미-디락 통계를 따르지만 스핀-통계 정리를 위반하는 복소 스칼라 장이므로 비물리적이다. (파데예프-포포프 고스트 참조)
양-밀스 이론을 양자화하는 방법 중 하나는 함수적 방법, 즉 경로 적분을 사용하는 것이다. 이러한 과정을 통해, n-점 함수를 생성하는 범함수를 다음과 같이 쓸 수 있다.[2]
:
여기서
:
는 장에 대한 것이고,
:
는 게이지 고정에 대한 것이며,
:
는 고스트에 대한 것이다. 는 고스트 장을 나타내고, 는 양자화를 위한 게이지 선택을 고정한다.
이 범함수를 통해 페인만 규칙을 유도할 수 있다. (페인만 도표 참조)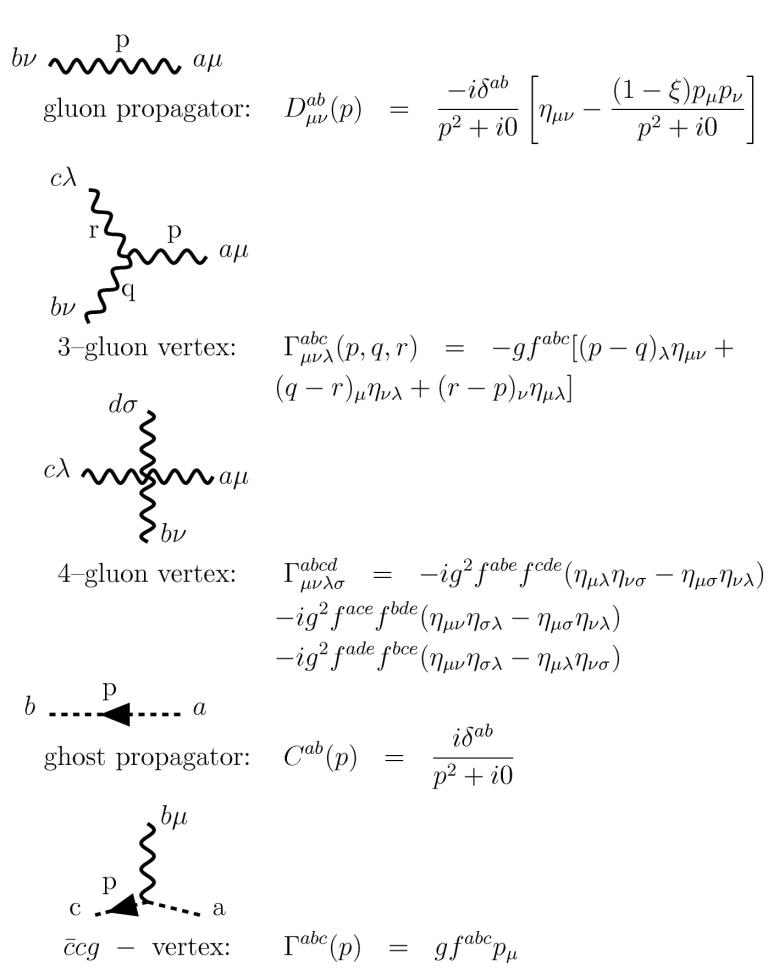
이러한 페인만 도표 규칙은 위에 주어진 생성 범함수를 이용하여 얻을 수 있다. 결합 상수 로 전개하고 함수 미분을 계산하면, 섭동 이론으로 모든 -점 함수를 얻을 수 있다. LSZ 축약 공식을 사용하면, 해당 과정의 진폭, 단면적, 붕괴율을 얻을 수 있다.[2] 이 이론은 재규격화 가능하며, 섭동 이론의 모든 차수에서 보정이 유한하다.[2]
양자 전기역학의 경우 게이지 그룹이 가환이므로 고스트 장은 분리된다. 비가환 게이지 군을 갖는 양-밀스 이론에서는 고스트 장이 양자 장 이론을 다시 쓰는 유용한 방법으로 나타난다.
7. 미해결 문제
양-밀스 이론의 수학은 매우 활발한 연구 분야이며, 사이먼 손턴 도널드슨의 연구를 통해 4차원 다양체에서 미분 가능한 구조의 불변량을 산출하는 등 중요한 역할을 한다.[12] 또한, 양-밀스 이론 분야는 클레이 수학 연구소의 "밀레니엄 문제" 목록에 포함되었다. 여기서 상금 문제는 특히 순수 양-밀스 이론(즉, 물질장이 없는)의 최저 여기 상태가 진공 상태에 관해 유한한 질량 간극을 갖는다는 추측의 증명으로 구성된다. 이 추측과 관련된 또 다른 미해결 문제는 추가적인 페르미온이 존재할 때의 색 가둠 속성을 증명하는 것이다.
참조
[1]
웹사이트
Yang-Mills & The Mass Gap
https://www.claymath[...]
2024-04-09
[2]
저널
Gauge theory: Historical origins and some modern developments
https://link.aps.org[...]
2000-01-01
[3]
서적
Mathematical Conversations: Selections from the ''Mathematical Intelligencer''
https://books.google[...]
Springer Science & Business Media
2012-12-06
[4]
서적
The Quantum Story: A history in 40 moments
Oxford University Press
[5]
저널
Conservation of isotopic spin and isotopic gauge invariance
[6]
arXiv
On Pauli's invention of non-abelian Kaluza-Klein Theory in 1953
[7]
memorial
Ronald Shaw 1929–2016 by Michael Atiyah (1954)
https://issuu.com/tr[...]
2017
[8]
논문
The problem of particle types and other contributions to the theory of elementary particles
University of Cambridge
1956-09
[9]
서적
Cosmic Anger: Abdus Salam – the first Muslim Nobel scientist
Oxford University Press
2008
[10]
저널
Mass and width of the lowest resonance in QCD
[11]
저널
Experimental status of the ππ isoscalar S wave at low energy: {{mvar|f}}0(600) pole and scattering length
[12]
저널
Regularization and renormalization of gauge fields
https://repositorio.[...]
[13]
저널
Yang and Mills (1954)
[14]
문서
On Pauli's invention of non-Abelian Kaluza-Klein Theory in 1953
[15]
문서
See Abraham Pais' account of this period as well as L. Susskind's "Superstrings, Physics World on the first non-Abelian gauge theory" where Susskind wrote that Yang-Mills was "rediscovered" only because Pauli had chosen not to publish
[16]
문서
微分とはその定義{{Indent|}}からも分かる通り、本質的に空間上の二点の値に依存する。従って、各点ごとに独立なゲージパラメタを持つ局所ゲージ変換の上で不変な項を作る事は、通常の微分からでは不可能である。その変化分を相殺するために、共変微分及びゲージ場が必要とされる。つまり、局所ゲージ不変性を要請する事と、ゲージ場の存在を要請する事とは同じ事である。field-strengthは、ゲージ場だけから作られるゲージ共変なテンソルとして一意に定まる。[[微分幾何学]]の言葉では、ゲージ場は[[接続 (幾何学)|接続]]、ゲージ場の強度は[[曲率]]となる。
[17]
저널
Conservation of isotopic spin and isotopic gauge invariance
1954-10
[18]
저널
Duality in supersymmetric Yang–Mills theory
https://archive.org/[...]
2002-12-14
[19]
저널
New superconformal field theories in four dimensions and N=1 duality
2001-01
[20]
저널
Lectures on supersymmetric gauge theories and electric-magnetic duality
1996-02
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
